Abstract, Composable, Extensible Data Model using Category Theory.
Abstracting data models from implementation with Category Theory gives independent life to data models, underpins data transfers with mathematical rigour and enables dream-like applications.
A unique method and approach to create Abstract Data Model using Category Theory, a branch of Mathematics, an Abstract Data Model that is composable, extensible and enforces structure preserving operations on data with Mathematical guarantee to data quality, provenance reliability and 100% constraint compliance at rest, during ingress, egress and facilitates existing data models of any type or non-data-model based data like IoT sensor data / text to inherit these Category Theoretical properties, including infinite data model composability and metadata extensibility among other properties.
Challenge addressed - what’s wrong with existing data model approaches:
Lack of abstracted separation of the Data Models (schema) is restrictive. Data Models do not have an independent existence outside the databases, as they are locked in the databases at the time of creation (schema). Unintended result of locking the data models in the databases resulted in disparate data models and information silos, the effects of which are severe. This one aspect of locking the Data Models in the native databases without abstraction resulted in immense inefficiencies across several aspects – from application integration to data engineering. This practice left several unintended consequences the entire industry is forced to live with for decades, a few examples:
Data Models do not have independent existence outside databases. The need for structured metadata is intense due to emerging business needs like data privacy, federation, residency. This cannot be addressed with traditional models without touching source data every time for every different purpose. Data Model abstraction is required to address this. This is more pronounced for Relational DB, which constitute the most in legacy enterprise systems - ERPs etc.
The models do not provide any certainty / guarantee required to establish confidence in data quality, reliability and lineage, despite being the origin of metadata, despite being the source of authority (data type, constraint definitions etc.,) severely affecting data reliability, privacy and lineage.
Once data are materialized over a data model, the interactions with data are not structure-preserving as the operations are directly carried with data and over time, data drifts away from set constraints in the data models, leading to data quality issues.
The data models play a central role representing the contours of business context, but the context is not freely discoverable and lost inside the data models (one must login to even see which data fields exist).
The models are not composable (formally like mathematical functions). Any enterprise environment is a composition of blocks of knowledge, but prevalent integration practices leave hundreds of overlapping knowledge blocks, not aware of one-another, created with redundant efforts for lack of composability in data modelling.
Reliance on ‘accidental’ data commonality across disparate data sets, instead of ‘planned’ reusability. Planned reusability is not supported naturally by current data model approaches as the native models (and databases) are not designed for reusability. They are not interoperable (even homogenous databases), not extensible due to both technical and commercial reasons.
Context of business intent gets locked in the heads of a few developers involved in the data model definition. This knowledge is lost or hidden in various native data models.
Even when the knowledge is documented or original development teams are available, the models are not extensible without expensive development efforts which also tend to disrupt business continuity.
These models cannot be ported to other platforms without expensive manual efforts. The models are not portable even within same database environment. Porting across different data model types gets lossy and time-consuming. This is even worse with porting across vendors’ proprietary models.
The ‘context’ of data sources (metadata and related), is extremely simplistic in the current approaches (just a few words), is locked in the native database systems, cannot be extended with incremental information both technically (cannot change much once deployed e.g., RDBMS) and functionally (cannot add knowledge) without laborious integration efforts every time, only to result in yet another rigid set of metadata.
Lack of abstracted separation is restrictive. This proves to be expensive in several cases (scientific, pharmaceutical and consumer behaviour research studies) when it comes to reusability or composability.
The challenge is not just the contextual knowledge locked in data models that needs abstraction, but also the repercussions of locking data models itself, making data driven inferences for business/operational decisions ineffective, slowing down adoption of Cloud, Machine Learning and even IoT. Data Model, being such a fundamental building block, needs a different approach to address these challenges – it needs abstraction and mathematical guarantee to every operation conducted on the data it represents.
Solution: An Abstract Data Model that is portable, composable, extensible and reusable with Mathematical guarantee to data lineage and reliability.
Category Theory (a branch in Mathematics) comes in handy to create the Abstract Data Model approach to address the above issues elegantly and performantly. Category Theory is effective at structure preservation, structure transformation, porting, knowledge modelling and continuous context capture, successfully used in several scientific and mathematical fields.
The is an approach to create Category Theoretical Abstract Data Models (CTADM) which enables existing data models of any database to inherit strengths of Category Theory (portable, composable, extensible and reusable with mathematically guaranteed data reliability, constraint sanctity and lineage and other properties) to address above challenges.
This approach allows a data model to have its own existence, independent of implementation, unleashing several possibilities of immense value not possible before and opens a universal and elegant abstraction to data modelling. This approach lays the foundation for several data related extensions – like data privacy, residency, regulatory compliance, reliability, lineage and data sanctity (constraint sanctity, meta data sanctity and context sanctity), potentially saving millions of hours of data engineering.
This approach enforces ‘structure-preserving operations’ and enables all data related operations e.g, insertion, integration, migrations, transformations) to be done off the ‘data model’ instead of directly on ‘data’. This will ENSURE that such operations ALWAYS result in data model compliant data (data types, constraints, relationship definitions) at rest, during ingress and egress. And using Mathematical base to achieve this makes it more powerful – by assuring mathematical guarantee and accuracy to data relationships, transfers, transformations and data quality/reliability.
Category Theoretical Abstract Data Models (CTADM) acts as the central nervous system that connects siloed, disparate data models (distributed relational, graph, unbounded data from IoT devices, text data etc), unlike the ‘locked in with the database’ but ‘disconnected from materialised data’, non-descriptive like traditional data models.
CTADM is a live artefact that can continually evolve to model business context and contextual changes.
CTADM is connected to the underlying data and enforces 100% structure-preserving operations on data at rest, ingress and egress.
Category Theoretical Abstract Data Models have the below properties. They
Have independent (of databases) lifecycle – versions, extensions, evolution across time, yet synchronised with native database schema.
Are composable with mathematical certainty
Provide mathematically guaranteed reliability
Provide mathematically guaranteed lineage.
Are extensible with other data models and data sources
Enable ‘planned’ reusability, instead of relying on ‘accidental’ data commonality across disparate data sets.
Allow constraints in a formal, expressive, rich language
Enforce constraint integrity during run-time; during transformation;
Provide assurances of data quality by construction
Work with existing data models (of existing databases of any type) and new data models.
Compose and connect with other data model types (relational, graph, document, text, columnar).
Dynamically, ad hoc establish relationships among data sources.
How does the proposed solution approach work?
The proposed approach considers Category Theory, a branch of Information Theory in Mathematics, as the basis. (An Introduction to Category Theory is attached in Related Documents). Note: ‘Category’ here denotes the Category Theoretical concept of Category, with its properties, not the general sense of category.
The proposed approach creates abstraction of existing data models of any type (any relational, graph, columnar, document etc. data models) as Categories and creates a universal categorical data model that represents the stated, discovered, user or machine learning suggested relationships among the incoming data models, enabling the native data models to inherit the Category Theoretical properties - i.e., mathematical guarantee to data structure, quality, sanctity, lineage etc., while allowing existing database applications to run normally.
The approach is detailed below.
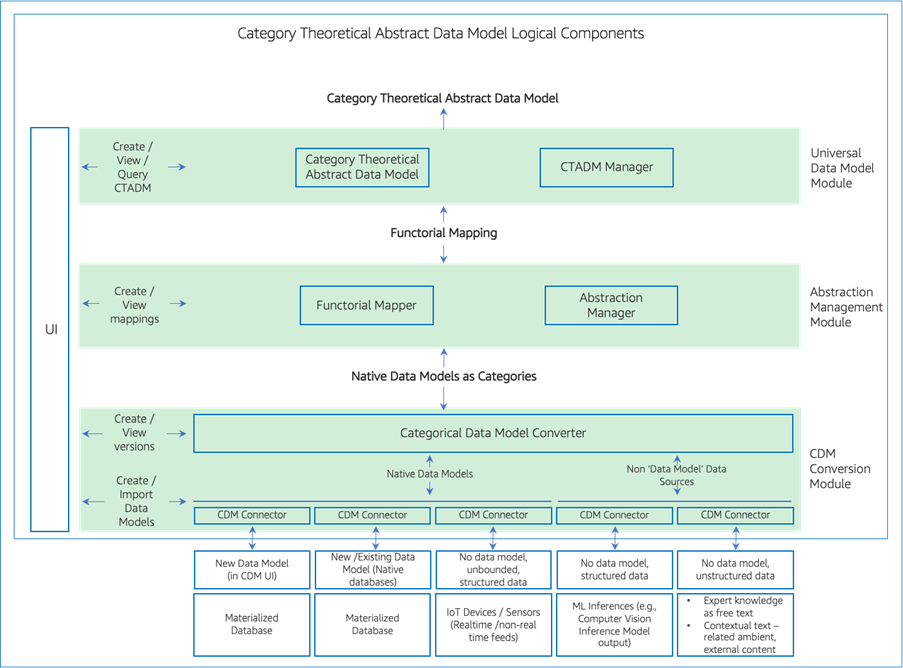
Diagram 1: Category Theoretical Abstract Data Model
The approach has the following modules – CDM Conversion Module, Abstraction Management Module and Universal Data Model Module, as shown in Diagram 1.
1. Category Data Model (CDM) Conversion Module:
This module converts native data models into mathematical (Category Theory based) Categories. The created Categories represent the native data models with 100% fidelity (100% lossless), including the entities, data types, relationships, constraints and primary /foreign keys. This modules comprises two sub-modules: Categorical Data Model Convertor and CDM Connectors.
The inputs to Categorical Data Model Converter sub-module are native data model definitions (schema), which can be ingested (e.g., from native databases), or defined in a UI associated with this module. This sub-module comprises
The logic required to convert native data model of any type (relational, graph, columnar and document) into Categories.
The logic required to convert unstructured data not bound by a data model into a Category, e.g., context of a business scenario in the form of unstructured tribal knowledge of expert users as free text.
The logic required to convert data which is structured but not bound by / attached to a data model (device, sensor data), streaming or otherwise. e.g., data from an IoT device / Computer Vision inference that can be attached to the context of other structured data model ad hoc.
This sub-module also creates Categories of the materialized ‘data’, in addition to creating Categories of ‘data model’, and keeps record of the relationships between the ‘Categories of data models’ and ‘Categories of data’.
Further, the CDM Conversion module also includes CDM Connectors sub-module.
CDM Connectors manage ingestion of native data models, keep track of changes to data or data models, and communicate the same to CDM Convertor. This enables CDM Convertor module to keep the created Categories (of native models) synchronized with native models and also keep track of native data model versions, along with data changes with reference to the data model changes, if any.
The CDM connector also manages creation of new CDM Models. Users can create data models of any databases in the CDM Module’s UI which get translated to the native DBs required instructions (e.g., SQL) to create the tables / database and also are passed on to CDM Convertor to create a CDM, thus creating both native DM and CDM together.
In summary, the output of this module is a Category for every input native data model and materialized / instantiated data set.
This can be used for existing data models and also for new data models.
2. Abstraction Management Module:
Abstraction Management Module takes the Categories as inputs and establishes relationships among the input data models and data sets with mathematical formality (called Functors, relationships among Categories). This abstraction enables several advantages not possible in the current approaches. 1/ Allows interaction between disparate data models, not just within the same database type but even across database types (relational, graph, document etc.) 2/ Allows to maintain changes to the relationships across time (versions) 3/Enables to track changes to materialised data across time, with reference to the data model changes.
This is achieved by two sub-modules.
Functorial Mapper: Functorial Mapper establishes relationships across the Categories. This includes relationships among homogenous databases (e.,g relationships among relational tables in the form of Foreign Keys etc.,) and also relationships across heterogenous databases (e.g., relationships among relational and graph schema).
The bases for such relationships are derived from:
Hidden relationships discovered by Category Theoretical models (inherent property – base on path equivalencies. Please refer to Introduction to Category Theory in Related Documents).
The relationships as defined in the incoming Categories – e.g, foreign keys, joins.
Manual inputs in the UI, in the form of corrections or creating new relationships (that hold true for the data model and the instantiated data, validated and enforced at row level, a natural property derived from Category Theory).
Relationships suggested based on inference models – e.g., semantic affinity (field names that may be same but worded differently – customer ID vs cust ID) using NLP or any similar mechanism.
The Functorial Mapper consumes all these inputs and creates the relationships among incoming Categories (i.e., the Categories of native data models created by CDM Convertor).
Abstraction Manager: Abstraction Manager manages 1/ abstraction and translation among different data models – e.g., relational data models vs graph data model. This is required to interoperate (convert) among different data models – e.g., from relational to graph. 2/ abstraction with the Category Theoretical Abstract Data Model (CTADM), described in the next section. This is required to maintain independence of underlying native data models from the CTADM while keeping a synchronized reference to the CTADM.
The Abstraction Mapper also keeps track of all the versions – versions of mapping, data models and data sets.
3. Universal Data Model Module:
This module constitutes Category Theoretical Abstract Data Model Creator and CTADM Manager.
Category Theoretical Abstract Data Model Creator creates a Categorical Data Model consuming the Native Data Model Categories and Functorial mapping from the lower layers, resulting in Category Theoretical Abstract Data Model that can have independent existence while closely being related to native data models.
CTADM Manager manages the models (CTADM), the models’ versions and the models’ relationship with reference to data. CTADM Manager also enforces compliance of data at rest, during ingress and egress with data model definitions (data types, constraints, relationships, reference conditions, computation functions).
The resulting Category Theoretical Abstract Data Model has the following unique characteristics due to the approach (ie. Abstraction) :
This enables Abstraction of the data model – i.e., the data model can be accessed, extended, reused, composed and translated by any database application irrespective of data models, or anyone interested. The enabling mathematical foundation provides exactly one way to interpret the model (definitions, relationships, constraints etc.) and its changes across time.
A unified data model, with mathematically guaranteed unique path among all incoming data models, respecting all constraints defined in the native data models and the complex, overlapping relationships, including the hidden relationships discovered by Functorial Mapping module and user recommended relationships.
It is not necessary to have multiple input data models to create this abstract data model. Even with one input data model, the output will be a Category Theoretical Data Model that inherits the Category Theoretical properties and allows future extensions, compositions etc.
Such unification of data models also conforms with the materialised data from data sources, not just the underlying data models, i.e., every cell / row is checked for compliance with the data model’s conformance rules (constraints, relationships), highlighting any non-compliance.
This Abstraction enforces constraint integrity on data at rest and during ingress / egress. The abstraction also enforces structure-preserving operations (e.g., integrations and migrations) as all data related activities are enabled to be done ‘through the data model’ instead of directly on ‘data’ bypassing the data model in the traditional approach. This will ensure constraint integrity, i.e., any such activities always result in data model compliant data (data types, constraints, relationship definitions). And using Mathematical base to achieve this makes it powerful – by assuring of mathematical guarantee and accuracy to data relationships, transfers, transformations and data quality / reliability.
This approach also enables accurate lineage without touching the native database but still maintaining the entire chain of relationships – i.e., original native data model, translated data model, any compositions, transformations, extensions recorded as versions with 100% traceability, mathematically guaranteed provenance.
While creating a unified abstract data model with mathematical guarantee itself is a step change, this approach also bestows the following Category Theoretical properties to the legacy data models:
Model Extensions: The proposed approach allows data models to be extended flexibly and incrementally by appending additional data models (relational, graph – homogenous or heterogenous) incrementally as and when required, at the CTADM level, without touching the underlying native data models. Note that relationships can exist between relational and non-relational data sources. Relationships can also be established ad hoc, dynamically – eg., attaching data from IoT sensor data / Computer Vision inference models to a relational/any data model instantly.
This enables dynamic, flexible, ad hoc data modelling capacity.
Custom Metadata: The sparse metadata from the native schema definitions can be appended with more descriptive metadata across time, anytime, collaboratively by distributed teams, outside the database applications and still have reference to the native data models but without touching the native data schema or related database tables. E.g. a database schema can be extended to denote some fields as Personally Identifiable Information, or appending any rich context (e.g. external data feed) to any attribute / field without touching the native schema.
This makes the Data Models and associated metadata discoverable, extensible and composable by all types of users – business, functional etc., not just technical users.
Mathematically guaranteed Reliability: Complex ‘structure-preserving data integration operations’ with assurances of ‘data quality by construction’ (during data transformation or mapping) allowing heterogeneity of exposure in different data sources.
Composability with mathematical certainty: Data Models, even heterogenous, can be composed to form composite data models, just like mathematical functions, with associated guarantees (associative rule etc.,)
Formality: Rich language for constraint and relationship definitions, functional declaration inherited from the mathematical base.
Versions: Changes to native data models and CTADM are versioned, with relationships among them maintained accurately.
Materializations: History of materialization – i.e., underlying data changes are also versioned with reference to data model changes.
Enables ‘planned’ reusability, instead of relying on ‘accidental’ data commonality across disparate data sets.
Assures data quality by construction (during data transformation / mapping)
While these are the most impactful properties inherited, several other powerful properties are also inherited from Category Theoretical approach (Please refer to the Introduction to Category Theory document in Related Documents).
Applications of the this approach:
Anchoring all integration activities around an abstracted, reusable, extensible data model goes beyond solving the above issues and unlocks unprecedented business value.
The solution is not simply a layer of abstraction that liberates the data models but
introducing a hygiene of re-thinking data modelling approach as reusable, composable, extensible, portable, and how this affects the many touch points of such data models.
facilitating the numerous enterprise integration and data usage capabilities unleashed by this abstraction.
This approach impacts application design, query design and UI design for the target applications because of this approach.
The approach results various layers of functionality exposed through user interfaces to,
Connect with data sources or metadata sources (data models in 3rd party systems),
Allow the users to view, explore schemas,
Collaboratively evolve schemas working on a shared artefact among different teams like data analyst, business analyst and programmer teams etc,
Conclusion: Unlocking the data models from implementation with Category Theory based data model abstraction, besides underpinning data kinetics with mathematical rigour, enables the following use case:
Given a target data model and 1000s of source data models, arriving the unique mapping that is accurate, mathematically guaranteed automatically.
Given a target data model and 1000s of source data, check every row/cell automatically to confirm if the target model is possible and highlight data gaps, quality issues, automatically.
Given 1000s of data sources, arrive at normalized data model and data automatically or arrive at Data Frames automatically, with mathematical guarantee.
Given 1000s of data sources, arrive at possible features
Given 1000s of data sources, a list of required features, check if such features can be materialized check every row/cell and highlight data gaps.
Export: The proprietary data models locked in proprietary vendor schema like Power BI, can now be exported to any target of choice, expediting migration to Cloud.
Cloud Refactor: Several organizations are transitioning to Cloud services both on the source side (source side persistence moved to AWS Aurora DB) and on the target side (to Teradata on AWS S3), necessitating a complete revisit of source schemas, targets schemas and transformations for every source-destination combination, resulting in time-consuming manual efforts. This module can automate and expedite the whole process and buffer the transitions across source-destination combinations.
Translate: Businesses having complex environments with multiple integration platforms / BI systems need to translate among proprietary models, across versions and reuse the constituents (source schema, transformations etc.). Translate addresses this need by translating and exposing the constituents of one model (e.g. Informatica model) to be explored in other environments (e.g. AWS Glue + S3), providing access to metadata (schema), source extracts, target data loads and common transformations. This saves the heavily manual, error prone approaches prevalent and even entirely obviates a few steps – e.g., mapping of source schema by data analyst several times, the same activity repeated by integration developer several times, both disconnected and introducing mapping errors en route.
Extend: ‘Stability’ of enterprise integrations depends on the stability of the Data Model, that need not be dropped with business changes – incremental or otherwise. This delivers the functionality required to enable Abstract Data Models to be used for incremental enterprise integrations, infusing a new life into the stability of such integrations, leveraging composability.
Query: This delivers the functionality required to achieve database virtualization by querying off Universal Abstract Categorical Data Model with query federation; query performance enhancements by leveraging native advantages like the dot operator; and implementing MPP by prefetching data subsets leveraging data relationships.
‘Enforcing’ mandate compliance during execution (e.g. GDPR, PII), capturing exceptions before committing.
Enforcing business rules (e.g. cross-tenanted applications’ data exposure), avoiding post facto legal hassles.
Maintaining and translating extended lineage requirements for data-sensitive scenarios (source data lineage and transformation lineage that make the research results replicable across original, changed or incremental data sets), preventing information loss during transformations and saving significant manual efforts in scientific, pharmaceutical and consumer behaviour research etc.
Collaborative mapping with canonical meaning of business data is a catalyst in triggering network dependent technologies like Blockchain or data-quality intensive technologies like AI.
Note: The above concepts, applications, user experience examples are protected by Intellectual Property Rights owned by Surendra Kancherla, barring the ones protected, owned or open-sourced by Conexus, CQL and their personnel.